Chi legge questo articolo lo fa a suo rischio e pericolo, viene pubblicato qui solo come curiosità e spiega come sia possibile misurare in modo accurato e preciso una quota in montagna con una spesa di circa 60 euro, una buona dose di pazienza e un pizzico di matematica.
Mentre stavamo lavorando al Rifugio De Gasperi per l’adeguamento alle normative antincendio abbiamo lasciato sul poggiolo antistante al rifugio un ricevitore GPS per raccogliere dati.
Il ricevitore è stato posizionato più o meno a caso sul cordolo di cemento che sostiene il terrazzamento, quello che ci interessava era ricavare la quota esatta del piano antistante al rifugio.
Come qualcuno avrà già notato un ricevitore GPS lasciato nella stessa posizione per alcune decine di minuti (dalle 12:00:00 alle 12:29:59) raccoglie qualcosa di simile a quello che abbiamo visualizzato noi:
Soluzione autonoma ricevitore GNSS. Media: Lat 46°31’12.5751″ N, Lon 012°40’33.3990″ E, 1773.226 MSL
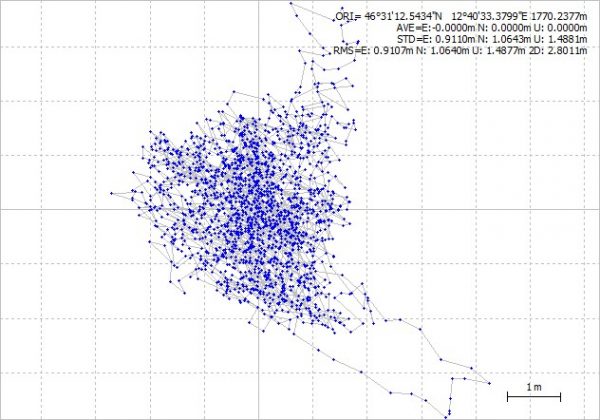
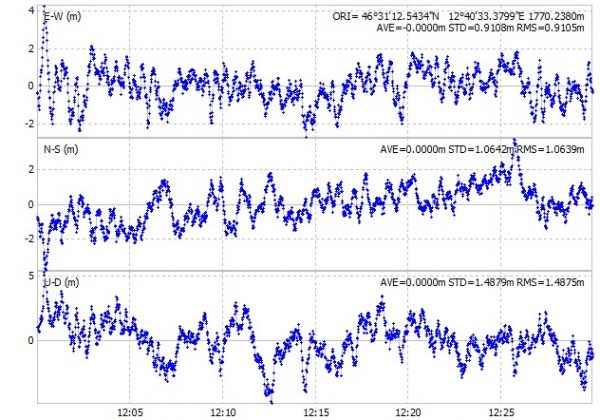
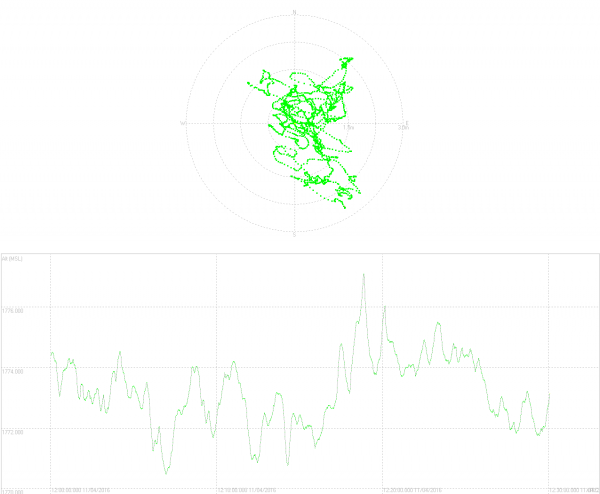
Come si può vedere il punto che rappresenta la soluzione “vaga” in modo piuttosto caotico, pur rimanendo in un cerchio di qualche metro di raggio, anche l’altezza rilevata oscilla. Ciò è dovuto agli errori di vario tipo che affliggono le misurazioni GPS e che variano in modo continuo. Questa è la soluzione che il ricevitore calcola in autonomia utilizzando i satelliti GPS (americani) e GLONASS (russi), in più applicando le correzioni che riceve via satellite dal sistema SBAS EGNOS (europeo).
Acronimi a parte, come si può vedere il risultato appare povero, almeno se vogliamo parlare di precisione di livello superiore. Già così comunque siamo oltre il livello attualmente raggiungibile da qualunque smartphone o gps commerciale.
La media di queste misurazioni è risultata essere:
Lat 46°31’12.5751″ N, Lon 012°40’33.3990″ E, 1773.226 MSL
[NB: attenzione se ripetete questo esperimento con uno smartphone è molto probabile che non vediate questo effetto, ciò è dovuto al fatto che spesso un telefono evoluto utilizza anche altri sensori per capire quando è fermo e quindi come posizione emette sempre una media degli ultimi dati ricevuti fino a quando rileva uno spostamento consistente o un cambio di velocità tramite giroscopi o accelerometri, inoltre spesso la quota è frutto della fusione dei dati di più sensori, incluso ovviamente quello barometrico]
Quindi ciò che possiamo fare finora è solo affidarci al ricevitore stesso ed effettuare una media su un gran numero di punti, ma ovviamente si può andare ben oltre, ed ora vediamo come.
Da qui in poi si noti che stiamo lavorando sempre sugli stessi dati raccolti nella sessione dalle 12:00:00 alle 12:29:59 del 4 novembre 2016… 1800 punti, uno ogni secondo(!).
Iniziamo quindi ad elaborare i dati raccolti. Quando parliamo di “dati” GNSS raccolti non parliamo di una semplice sequenza di punti, ovvero latitudine, longitudine e quota, ma, a differenza dei ricevitori commerciali, quello che abbiamo utilizzato è in grado di registrare i dati grezzi dei satelliti, tutti i dati grezzi, pseudorange, carrier phase e doppler. Ogni ricevitore GPS raccoglie questi dati internamente, la differenza è che il 99% li elabora e li trasforma in quello che serve all’utente, ovvero una “soluzione” PVT: punto, velocità, tempo. Ma non rende disponibili i dati grezzi.
Avere a disposizione questi dati ci consente di ripetere il calcolo della soluzione a posteriori aggiungendo altri dati e di confrontarli con quelli analoghi prodotti da una stazione GPS fissa presente nelle vicinanze. L’OGS ha una stazione che registra i dati di GPS e GLONASS sul Monte Varmost che dista circa 11 Km. L’antenna in questione ovviamente ha una posizione nota con grande precisione (talmente precisa che viene utilizzata per analizzare i movimenti della crosta terrestre).
Quindi confrontando i nostri dati con quelli della stazione fissa possiamo eliminare tutti gli errori comuni alle due posizioni Varmost – De Gasperi, lasciando da risolvere solo errori locali.
 |
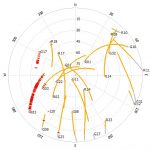 |
| Varmost, Skyplot | De Gasperi – Skyplot |
 |
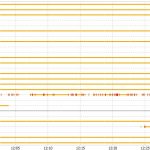 |
| Varmost, visibilità satelliti | De Gasperi, visibilità satelliti |
Nelle immagini sopra vedete come i ricevitori del Varmost e del de Gasperi (il nostro) vedano le costellazioni dei satelliti durante la mezz’ora in questione. Il nostro come si può notare ha la parte a nord ovest ostruita dal rifugio stesso e dalle Dolomiti Pesarine alle spalle, in più un paio di satelliti sono stati ostruiti da un abete e da un larice che hanno causato molti “cycle slip” nei dati (salti nella continuità delle osservazioni della fase) e che quindi sono stati esclusi dai calcoli. Ma rimangono comunque moltissimi satelliti in comune tra i due con osservazioni perfettamente pulite sulle quali lavorare.
La matematica che è nascosta in questo genere di procedimenti è piuttosto complessa, ma facciamo riferimento solamente ai grafici dei risultati.
Ecco cosa si ottiene con un primo passaggio facile, applichiamo la DIFFERENZIAZIONE al codice, questa sarebbe la classica soluzione DGPS:
Come si può vedere il risultato non sembra eccellente, il punto “vaga” comunque, ma quello che non si nota dal grafico è che la posizione media di tutti i 1800 punti ora è a 20 cm da quella che si rivelerà essere quella reale, mentre la quota si è portata anch’essa a valori più vicini al vero. In questo caso l’unica differenza è che abbiamo applicato le correzioni riferendoci alla stazione e non ai satelliti EGNOS, ma abbiamo lavorato sempre e solo sul codice del segnale GPS, ora iniziamo la parte difficile.
Da qui inizia una piccola magia matematica, ma prima un breve premessa.
Finora abbiamo utilizzato il codice emesso dai satelliti per calcolare la posizione del ricevitore. Si noti che le incognite che dobbiamo trovare sono quattro, tre per la posizione nello spazio del ricevitore e una quarta che è lo scarto tra l’orologio poco preciso del ricevitore e quelli atomici dei satelliti, quindi sono necessari almeno quattro satelliti.
Ogni satellite emette un proprio codice radio che lo identifica e con il quale ci dice la sua posizione, il ricevitore in base a quello che legge in questo codice per quattro diversi satelliti elabora la propria posizione nello spazio.
Questo tipo di posizionamento si dice appunto “di codice”, ma con le correzioni EGNOS e DGPS ne abbiamo esaurito le possibilità, almeno quelle semplici e siamo arrivati alla precisione massima consentita.
Per aumentare la precisione ora dobbiamo abbandonare il “codice” emesso dai satelliti e leggere la fase della portante radio che li trasporta, ovvero dobbiamo conteggiare le singole onde radio tra il ricevitore ed i satelliti. In pratica sapendo che le onde radio della portante sono lunghe 19.05 cm le contiamo e le moltiplichiamo per la lunghezza d’onda appunto, ottenendo la distanza e aumentando la precisione di circa 100 volte rispetto al metodo che utilizza il codice radio.
Il trucco in questo caso sta in un semplice calcolo matematico che consiste nell’eliminare alcune fonti di errori e le parti frazionarie delle onde radio nelle misure considerando le “differenze doppie” tra due ricevitori e più satelliti, complesso da spiegare, ma l’unica cosa che rimane alla fine è stabilire quale sia il numero intero di onde tra la nostra antenna ed i satelliti.
Ovviamente il secondo ricevitore al quale ci appoggiamo per fare di nuovo le “differenze” e semplificare il più possibile le cose per noi è sempre quello del Monte Varmost!
Questo tipo di applicazione, RTK, è nota da molti anni, ma finora era appannaggio di topografi professionisti con strumentazioni del costo di decine di migliaia di euro.
RTK, Real time Kinematic, ha un piccolo difetto, visto che le onde sono tutte identiche e necessario capire “quale onda stiamo conteggiando”, presuppone che si risolva la cosiddetta “ambiguità di fase” ovvero che si riesca a capire il numero intero di onde della portante tra il satellite e l’antenna del ricevitore.
Della verifica di questo conteggio se ne occupa un algoritmo matematico.
Durante i calcoli RTK lo stato delle soluzioni trovate passa da SINGLE (rosso) se la soluzione è ottenuta senza alcuna differenziazione a FLOAT (arancio) nel caso che detto conteggio non sia intero a FIX (verde) nel caso lo sia. Con lo stato di FIX la precisione aumenta di almeno due ordini di grandezza rispetto al ricevitore in modalità autonoma, ovvero circa 100 volte!!!
Per riuscire a raggiungere lo stato di FIX e risolvere l’ambiguità di fase è necessario un periodo di inizializzazione durante il quale vengono confrontati i dati delle due stazioni e verificati alcuni parametri in base ai quali si può stabilire se l’ambiguità sia risolta o meno.
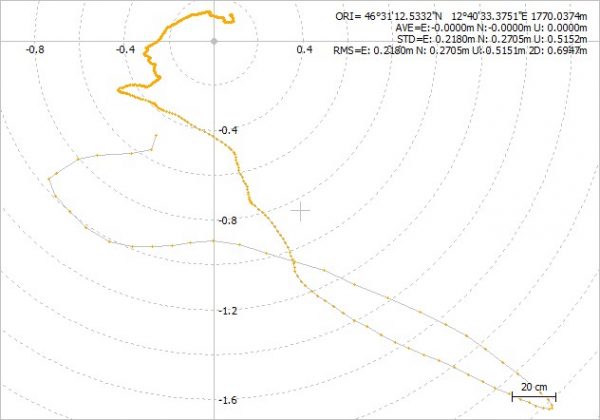
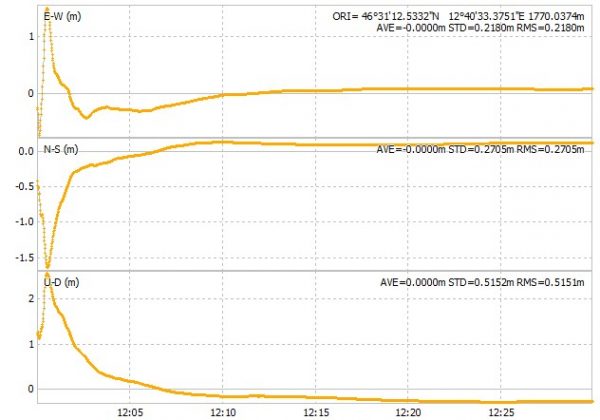
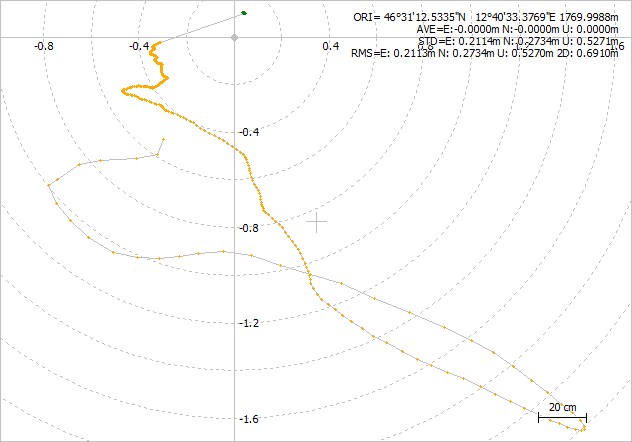
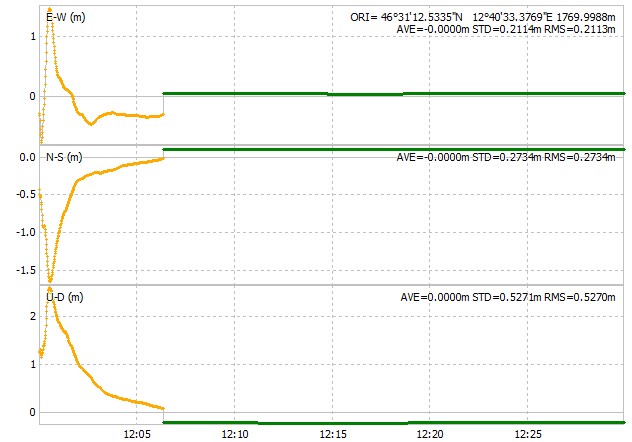
Ecco cosa succede se analizziamo i dati registrati in un primo modo molto semplice, rinunciamo alla soluzione delle ambiguità e lavoriamo solo in modalità FLOAT:
Già meglio vero? La prima figura mostra come i punti raccolti dal ricevitore si accumulino nell’intorno di circa 30/40 cm di un punto. Anziché disordine ora c’è un reale tentativo di convergere verso la verità. Il sistema pulisce la soluzione dagli errori man mano che analizza i punti.
Come detto abbiamo conteggiato le singole onde delle portanti del segnale senza verificare la “ambiguità integrale”.
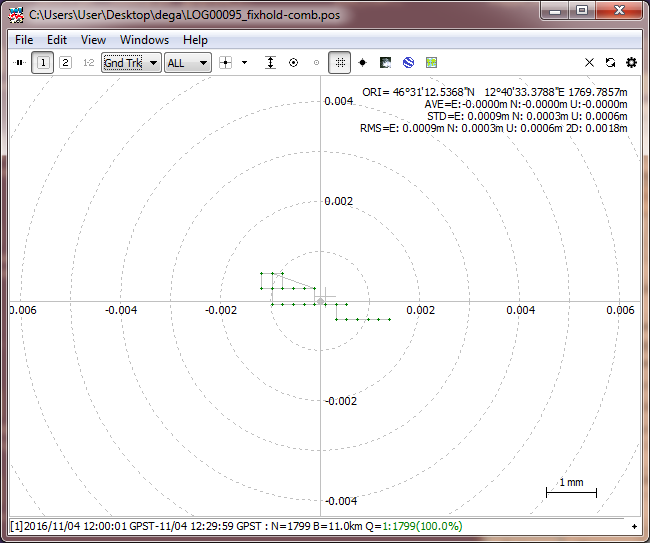
Ed ora la magia finale, premiamo sull’acceleratore a fondo e cerchiamo di applicare tutti gli strumenti matematici a disposizione, risolviamo anche le ambiguità:
La differenza è il piccolo gruppo di punti verdi in alto, rappresentati nella seconda figura dalle linee in verde, come vedete alle 12:06:30 secondi succede la magia, il sistema raccoglie dati a sufficienza per riuscire a conteggiare con estrema perfezione ogni singola onda di ogni singolo satellite utilizzato nei calcoli, portando la precisione del punto a livello del centimetro!
Ora la maggior parte dei punti sono raccolti nel piccolo puntino verde in alto e rappresentano la perfetta convergenza delle misure. Il sistema è in stato di FIX!
Ma non basta ancora, non siamo del tutto soddisfatti, visto che noi stiamo lavorando da casa e rifacendo il lavoro del ricevitore possiamo pure invertire il senso del tempo: partire dalle 12:00, andare alle 12:30 e poi tornare indietro per verificare ogni singolo punto sia in andata che in ritorno. In più possiamo applicare ulteriori dati al sistema, dati disponibili presso enti di ricerca, possiamo inserire le orbite ultra precise dei satelliti, i file che sistemano le piccole imperfezioni degli orologi, e perfino delle correzioni che considerano la rotazione terrestre… può sembrare incomprensibile, ma a questo livello di precisione ogni singolo elemento aggiunto alla computazione può aiutare… ed ecco quindi il risultato finale:
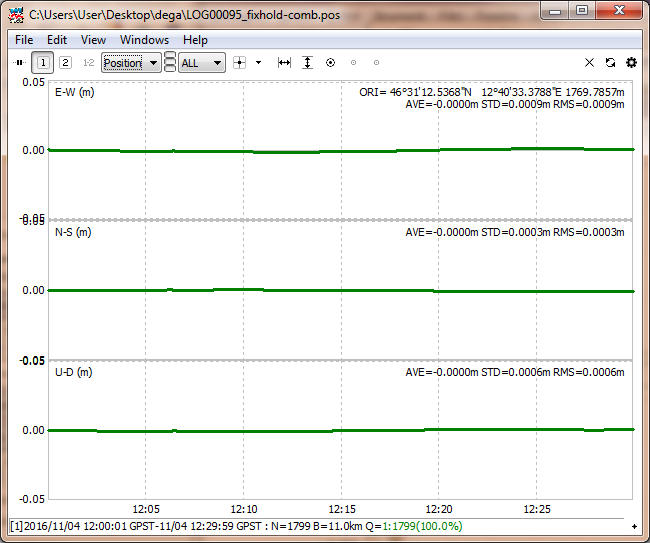
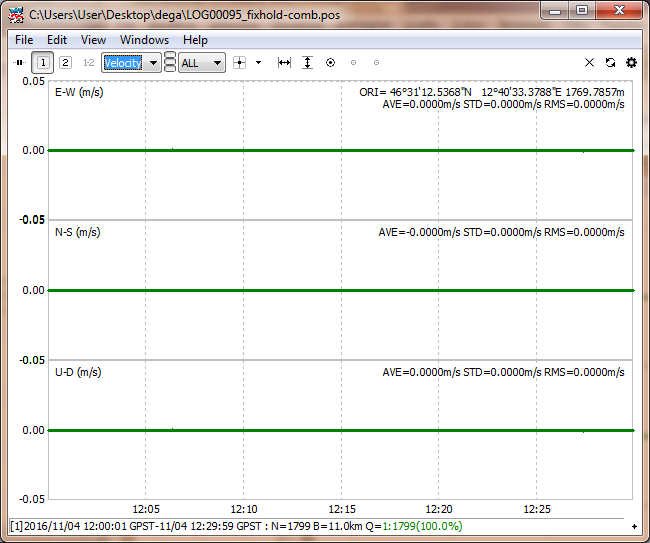
Ora… guardate BENE la scala dell’immagine, 1 mm!!! 1800 punti GPS incastonati in un cerchio di un paio di mm, impressionante vero?
Subito sotto vedete le variazioni nord sud, est ovest, e up down… praticamente minime e nella immagine successiva le velocità (le cui eventuali variazioni danno le accelerazioni), ovviamente nulle!
Ecco… ora per favore considerate che… i satelliti si trovano a circa 20.000 Km di altezza e viaggiano a circa 10.000 Km/h, che tutti i calcoli (anche quelli di codice!) vengono effettuati su onde che viaggiano alla velocità della luce e che le cose si fanno così complesse che è perfino necessario correggere gli errori dovuti alla relatività generale e speciale!
Eppure è possibile una così perfetta convergenza di misure.
Ovviamente non possiamo arrogarci il diritto di dire che siamo precisi al mm, il nostro ricevitore e la nostra antenna non sono certificati, ma da prove effettuate su punti già rilevati con strumentazione professionale possiamo tranquillamente prenderci il “cm” di precisione.
Ora… se pensate che l’articolo sia finito avete sbagliato di grosso 😉 …
l’altezza che abbiamo rilevato per il Rifugio Fratelli De Gasperi e abbiamo stabilito che è esattamente 1XXX metri sul livello del mare (nel sistema ETRF2000 (2008.0)!!!) è sbagliata!
Ovvero, è giusta, ma è la quota ellissoidica, ovvero riferita all’ellissoide WGS84 proprio del sistema GPS. L’ellisoide è un modo matematico di rappresentare la terra come una sfera schiacciata, ottimo per velocizzare i calcoli, ma non rappresentativo della realtà.
Purtroppo dopo che ci siamo accorti che la terra non è piatta e abbiamo detto che è tonda ci siamo pure accorti che non è nemmeno poi così tonda, anzi, è piuttosto sbilenca, come un arancino fatto a mano. Quindi troppe menti e troppe nazioni si sono fatte in quattro per creare rappresentazioni matematiche di questa terra che facessero comodo a loro creando una confusione atroce. WGS84 è un metodo di rappresentazione della superficie terrestre che copre tutto il globo, ovviamente non può essere preciso ovunque, quindi in Italia si utilizza Italgeo 2000 che è il geoide che l’Istituto geografico militare ha stabilito essere legale in Italia.
Ora… cosa molto strana visto che la sua creazione è stata pagata con le nostre tasse il suo utilizzo non è libero e per averlo bisogna pagare, e molto.
Comunque sia … e termino… l’altezza riferita a questo geoide è di 1767 metri sul livello medio mare!
La cosa che sarà interessante nei prossimi 4/5 anni è che sarà possibile avere precisioni di questo genere ed anche maggiori in modo perfino più semplice grazie alla messa in orbita di altri satelliti e alla possibilità di lavorare su molteplici frequenze ad uso civile. Perfino elaborare sistemi di risoluzione delle ambiguità dove non sia richiesta la base di posizione nota, ma solo la ricezione di più frequenze.
Una nuova era del posizionamento di altissima precisione si sta aprendo a tutti.
Tutto ciò verrà applicato alla mappatura dei sentieri e dove possibile si raggiungerà una precisione ben al di sotto del metro, fino anche al decimetro, per accatastarli tutti.
Speriamo di non avervi tediato, ma solo incuriosito. E ci scusino i topografi se abbiamo peccato di semplificazione eccessiva.
% (lat/lon/height=WGS84/geodetic,Q=1:fix,2:float,3:sbas,4:dgps,5:single,6:ppp,ns=# of satellites) % GPST latitude(d'") longitude(d'") height(m) Q ns sdn(m) sde(m) sdu(m) sdne(m) sdeu(m) sdue(m) age(s) ratio 2016/11/04 12:00:01.000 46 31 12.51964 12 40 33.36291 1771.2455 2 9 0.8627 0.8503 1.4144 -0.6132 0.7968 -0.7246 0.00 1.1 2016/11/04 12:00:02.000 46 31 12.51753 12 40 33.36185 1771.2726 2 9 0.6143 0.6043 1.0068 -0.4353 0.5658 -0.5143 0.00 1.0 [...] 2016/11/04 12:06:11.000 46 31 12.53236 12 40 33.36117 1770.1007 2 9 0.0146 0.0237 0.0232 0.0071 -0.0114 -0.0111 0.00 2.7 2016/11/04 12:06:12.000 46 31 12.53239 12 40 33.36125 1770.0993 2 9 0.0145 0.0236 0.0231 0.0071 -0.0113 -0.0110 0.00 2.8 2016/11/04 12:06:13.000 46 31 12.53243 12 40 33.36138 1770.0969 2 9 0.0145 0.0235 0.0231 0.0071 -0.0113 -0.0110 0.00 2.8 2016/11/04 12:06:14.000 46 31 12.53248 12 40 33.36148 1770.0949 2 9 0.0144 0.0235 0.0230 0.0071 -0.0113 -0.0110 0.00 2.8 2016/11/04 12:06:15.000 46 31 12.53253 12 40 33.36160 1770.0922 2 9 0.0144 0.0234 0.0229 0.0071 -0.0113 -0.0109 0.00 2.8 2016/11/04 12:06:16.000 46 31 12.53258 12 40 33.36174 1770.0900 2 9 0.0143 0.0234 0.0228 0.0071 -0.0113 -0.0109 0.00 2.8 2016/11/04 12:06:17.000 46 31 12.53263 12 40 33.36187 1770.0874 2 9 0.0143 0.0233 0.0227 0.0071 -0.0113 -0.0109 0.00 2.9 2016/11/04 12:06:18.000 46 31 12.53269 12 40 33.36203 1770.0847 2 9 0.0142 0.0232 0.0227 0.0071 -0.0113 -0.0108 0.00 2.9 2016/11/04 12:06:19.000 46 31 12.53275 12 40 33.36217 1770.0824 2 9 0.0142 0.0232 0.0226 0.0071 -0.0112 -0.0108 0.00 2.9 2016/11/04 12:06:20.000 46 31 12.53279 12 40 33.36232 1770.0801 2 9 0.0141 0.0231 0.0225 0.0071 -0.0112 -0.0108 0.00 3.0 2016/11/04 12:06:21.000 46 31 12.53283 12 40 33.36244 1770.0774 2 9 0.0141 0.0231 0.0225 0.0071 -0.0112 -0.0108 1.00 3.0 2016/11/04 12:06:22.000 46 31 12.53674 12 40 33.37891 1769.7860 1 9 0.0005 0.0005 0.0008 -0.0004 0.0005 -0.0004 0.00 3.0 2016/11/04 12:06:23.000 46 31 12.53674 12 40 33.37891 1769.7860 1 9 0.0005 0.0005 0.0008 -0.0004 0.0005 -0.0004 0.00 3.0 2016/11/04 12:06:24.000 46 31 12.53674 12 40 33.37891 1769.7860 1 9 0.0005 0.0005 0.0008 -0.0004 0.0005 -0.0004 0.00 3.1 2016/11/04 12:06:25.000 46 31 12.53674 12 40 33.37891 1769.7860 1 9 0.0005 0.0005 0.0008 -0.0004 0.0005 -0.0004 0.00 3.1 2016/11/04 12:06:26.000 46 31 12.53674 12 40 33.37891 1769.7860 1 9 0.0005 0.0005 0.0008 -0.0004 0.0005 -0.0004 0.00 3.1 2016/11/04 12:06:27.000 46 31 12.53674 12 40 33.37891 1769.7860 1 9 0.0005 0.0005 0.0008 -0.0004 0.0005 -0.0004 0.00 3.1 [...] 2016/11/04 12:24:28.000 46 31 12.53674 12 40 33.37889 1769.7863 1 9 0.0004 0.0005 0.0007 -0.0003 0.0004 -0.0003 0.00 74.9 2016/11/04 12:24:29.000 46 31 12.53674 12 40 33.37889 1769.7863 1 9 0.0004 0.0005 0.0007 -0.0003 0.0004 -0.0003 0.00 74.9 2016/11/04 12:24:30.000 46 31 12.53674 12 40 33.37889 1769.7863 1 9 0.0004 0.0005 0.0007 -0.0003 0.0004 -0.0003 0.00 74.9 2016/11/04 12:24:31.000 46 31 12.53674 12 40 33.37889 1769.7863 1 9 0.0004 0.0005 0.0007 -0.0003 0.0004 -0.0003 0.00 74.8 2016/11/04 12:24:32.000 46 31 12.53674 12 40 33.37889 1769.7863 1 9 0.0004 0.0005 0.0007 -0.0003 0.0004 -0.0003 0.00 74.8 2016/11/04 12:24:33.000 46 31 12.53674 12 40 33.37890 1769.7863 1 9 0.0004 0.0005 0.0007 -0.0003 0.0004 -0.0003 0.00 74.9 2016/11/04 12:24:34.000 46 31 12.53674 12 40 33.37890 1769.7863 1 9 0.0004 0.0005 0.0007 -0.0003 0.0004 -0.0003 0.00 74.8 2016/11/04 12:24:35.000 46 31 12.53674 12 40 33.37890 1769.7863 1 9 0.0004 0.0005 0.0007 -0.0003 0.0004 -0.0003 0.00 74.7 2016/11/04 12:24:36.000 46 31 12.53674 12 40 33.37890 1769.7864 1 9 0.0004 0.0005 0.0007 -0.0003 0.0004 -0.0003 0.00 74.6 2016/11/04 12:24:37.000 46 31 12.53674 12 40 33.37890 1769.7864 1 9 0.0004 0.0005 0.0007 -0.0003 0.0004 -0.0003 0.00 74.6 2016/11/04 12:24:38.000 46 31 12.53674 12 40 33.37890 1769.7864 1 9 0.0004 0.0005 0.0007 -0.0003 0.0004 -0.0003 0.00 74.5 2016/11/04 12:24:39.000 46 31 12.53674 12 40 33.37890 1769.7864 1 9 0.0004 0.0005 0.0007 -0.0003 0.0004 -0.0003 0.00 74.4 2016/11/04 12:24:40.000 46 31 12.53674 12 40 33.37890 1769.7864 1 9 0.0004 0.0005 0.0007 -0.0003 0.0004 -0.0003 0.00 74.2